
Factorisation Class 8 Extra Questions Maths Chapter 14 Msr Blog
Answer (1 of 2) I am assuming that should be 9z^2 otherwise it cannot be two planes axbyczd_1=0 and axbyczd_2=0 are two parallel planes that are non The equation (xy)^24xy9z^2 is given To find, factors of (xy)^24xy9z^2 Solution, The factors of (xy)^24xy9z^2 is (xy9z)(xy9z) We can simply factorize the equation (xy)^24xy9z^2 by using identities (xy)²4xy9z² (ab)² = a²b²2ab x²y²2xy4xy9z² x²y²2xy9z² (xy)² = x²y²2xy
(x+y)^2-4xy-9z^2
(x+y)^2-4xy-9z^2-Simple and best practice solution for 6x^24xy3y^2=28 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homeworkFactorise 9 z2 x24 x y 4 y2 Login Study Materials BYJU'S Answer;
2
7x2 (3x2y) 5y2 (3x2y) 4xy (3x2y) 21x314x2y 1 5 x y 2 1 0 y 3 12x2y8xy2 21x3 26x2y 7xy2 10y3 en pocas palabras descarga ph0t0math xd A Darmaidayxx y otros 31 usuarios les ha parecido útil esta respuesta heart outlined heart outlined Factorisation ICSE Class9th Concise Selina Mathematics Chapter5 with Exe5 A, Exe5 B, Exe5 C, Exe5 D and Exe5 E Solved QuestionsIf x, y and z are real and different and u = x^2 4y^2 9z^2 – 6yz – 3zx – 2xy, then u is always
Factorisation Class 8 Extra Questions Maths Chapter 14 Extra Questions for Class 8 Maths Chapter 14 Factorisation Factorisation Class 8 Extra Questions Very Short Answer Type Question 1 Find the common factors of the following terms (a) 25x2y, 30xy2 (b) 63m3n, 54mn4 Solution (a) 25x2y, 30xy2 25x2y = 5 × 5 × x × xकारक` 16x^24y^29z^216xy12yz24xz` Click here to get PDF DOWNLOAD for all questions and answers of this chapter RS AGGARWAL Class 9 FACTORISATION OF POLYNOMIALS6 Tìm các số nguyên x, y, z thỏa mãn x y z = 3 và x 2y 2 z 2 = 1 7 Cho x 3 x = 2x 2 Tính giá trị của P = x 10 1 8 Tìm GTLN của P = 3x x 2 1 9 Tìm số nguyên n sao cho 3n 3 10n 2 5 chia hết cho 3n 1 10 Cho a b = 2 và a 2 b 2 = 2 Tính a
(x+y)^2-4xy-9z^2のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 | 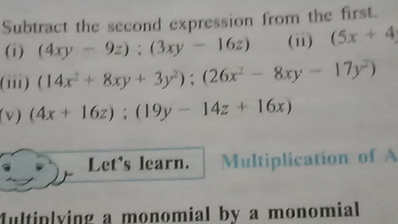 |  |
 |  |  |
「(x+y)^2-4xy-9z^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | 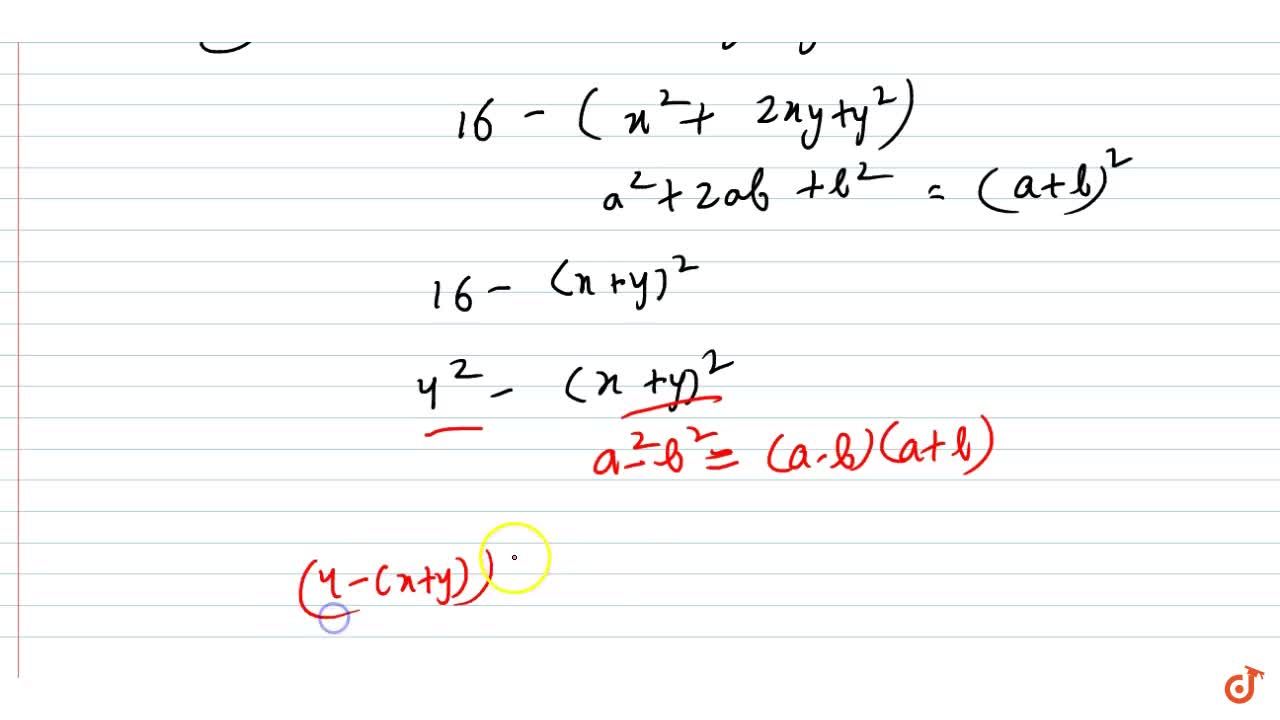 |
 |  |  |
「(x+y)^2-4xy-9z^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「(x+y)^2-4xy-9z^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | 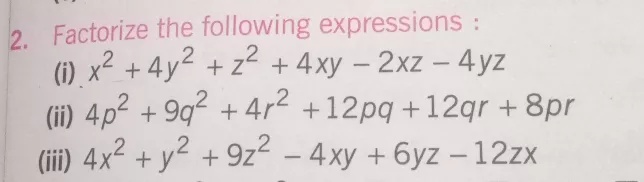 |
 | ||
「(x+y)^2-4xy-9z^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
「(x+y)^2-4xy-9z^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「(x+y)^2-4xy-9z^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「(x+y)^2-4xy-9z^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「(x+y)^2-4xy-9z^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | 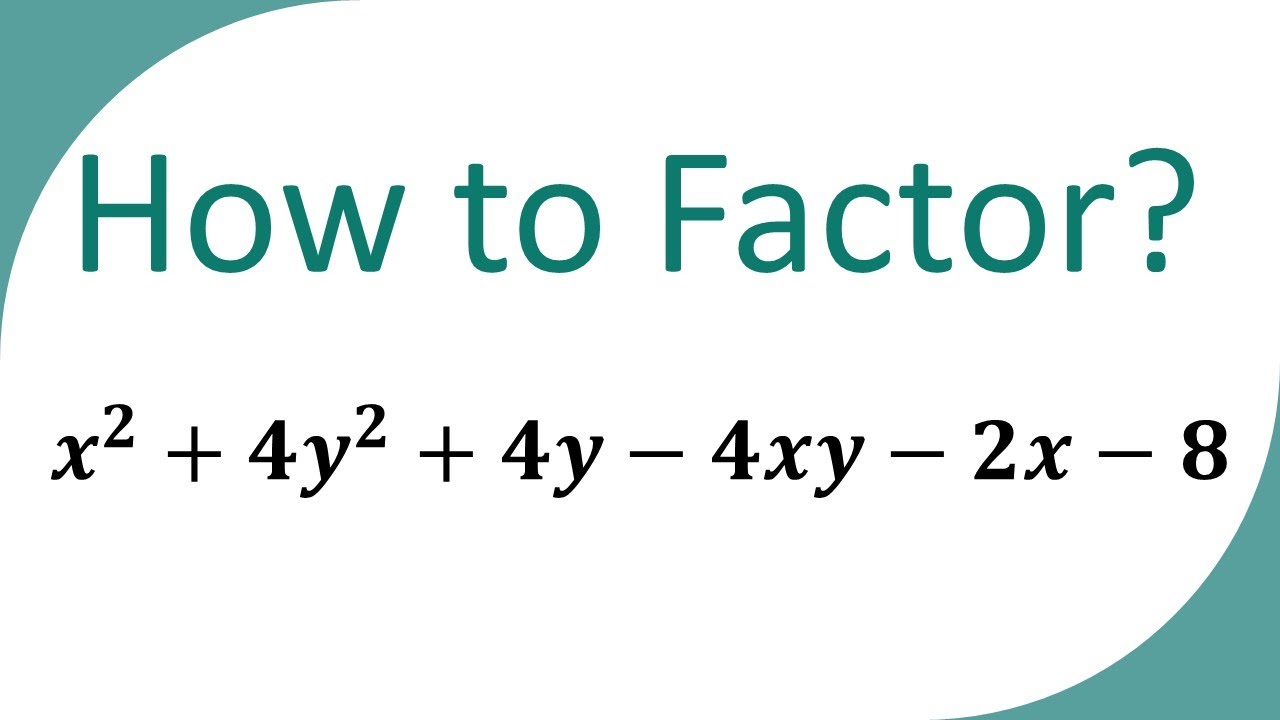 |
 |  |  |
「(x+y)^2-4xy-9z^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 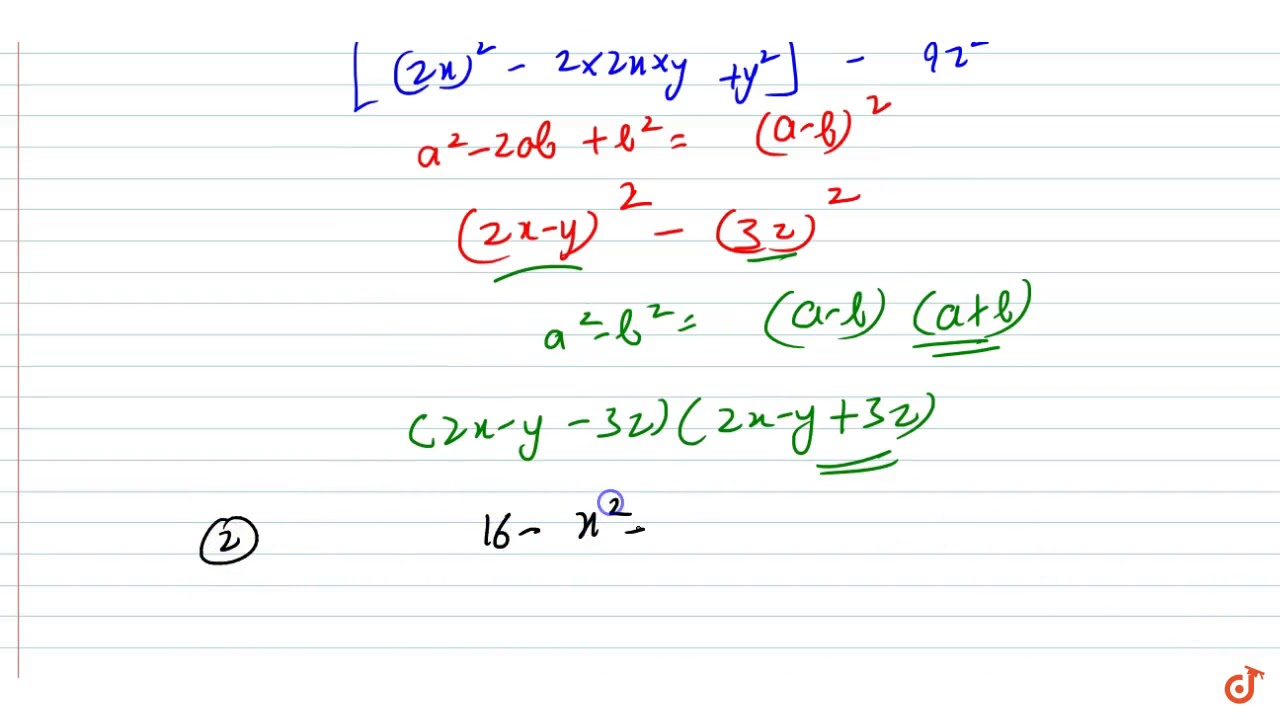 | |
 |  | |
 |  | 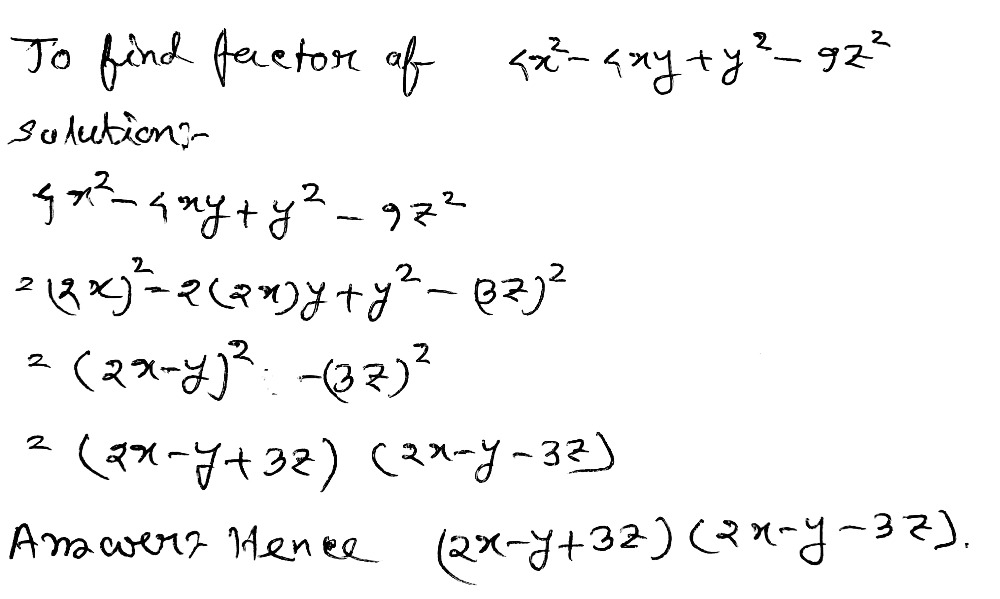 |
「(x+y)^2-4xy-9z^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
「(x+y)^2-4xy-9z^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |
The square of ( 2 x − 3 y z) is equal to 4 x 2 9 y 2 z 2 − 1 2 x y − 6 y z 4 z x State whether the statement is True or False The square of ( 2 x x 1 1) is equal to 4 x 2 x 2 1 5 x 2 4 x $$8x^68y^68z^67x^3y^37y^3z^37x^3z^318x^2y^2z^29x^4yz9y^4xz9z^4xy\ge 0$$ $$45x^69x^4yz45x^2y^2z^245y^69y^4xz45x^2y^2z^245z^69z^4xy45x^2y^2z^235(x^6y^6z^6)315x^2y^2z^2\ge 0$$ $$45(x^2(x^2yz)^2y^2(y^2zx)^2z^2(z^2xy)^2)35(x^6y^6z^63x^2y^2z^2)7(x^3y^3y^3z^3x^3z^3
Incoming Term: (x+y)^2-4xy-9z^2,




0 件のコメント:
コメントを投稿